資料科學從頭學(五) Linear Regression
(文章內容皆為記錄本人之學習過程,非以分享為目的)
1.數學基礎:
微積分、線性代數、統計學之檢定
2.用途:
1)迴歸分析屬於多變量分析的一種,所謂多變量分析是用於分析多個變數間的關聯。
2)迴歸分析分為線性與非線性,主要用於連續尺度,且至少一個相依變數的問題(獨立變數可以是一個或多個),針對離散的變數另有變化形式的羅吉斯回歸...等方法處理。
本篇文章純探討線性回歸中的 Simple Linear Regression、Multiple Linear Regression
p.s.
相依變數:又稱反應變數,就是真正想比較、想了解的東西。
獨立變數:又稱解釋變數,想藉由本因素找出與相依變數的關聯性。
3)統計學亦有很多迴歸的章節,針對廣義線性模型分類如下
1.數學基礎:
微積分、線性代數、統計學之檢定
2.用途:
1)迴歸分析屬於多變量分析的一種,所謂多變量分析是用於分析多個變數間的關聯。
2)迴歸分析分為線性與非線性,主要用於連續尺度,且至少一個相依變數的問題(獨立變數可以是一個或多個),針對離散的變數另有變化形式的羅吉斯回歸...等方法處理。
本篇文章純探討線性回歸中的 Simple Linear Regression、Multiple Linear Regression
p.s.
相依變數:又稱反應變數,就是真正想比較、想了解的東西。
獨立變數:又稱解釋變數,想藉由本因素找出與相依變數的關聯性。
3)統計學亦有很多迴歸的章節,針對廣義線性模型分類如下
4)多變項線性迴歸的變數選取是一個值得探討的重點主題,其嚴重影響模型的擬合度與解釋性。
3.理論:
Linear Regression 即為用一條直線來擬合點位資料,而縱軸(Y軸)通常是我們比較關心的相依變數,X軸是用來尋找關係的獨立變數,可以一個或多個,也可以多方嘗試找到最好的組合。
該直線的表示方式如下:
上圖可知簡單線性迴歸是多變項線性迴歸的一個特例。
參數估計方法分為最小平方估計法(Least squares estimate method),也就是讓每個真實資料點的y值(相依變數)與擬合線的距離平方總和最小化,此問題可用多變函數求極值的數學方法求解:
上式Q為差的總和,分別對各參數偏微分後可以得到k+1個多項式,如下:
以上可以用正規方程(Normal equation)或是梯度下降法(Gradient descent)來解,但一般特徵不太多的話,用正規方程的效果會比較好,如下:
解完參數後即可帶回方程式,並得到我們的直線。
4. 討論:
1)模型基本假設:
a.線性(Linearity):獨立變數與相依變數為線性關係。
b.條件常態分布(Multivariate normality):
若給定獨立變數後,相依變數呈現常態分佈,即誤差項也應該服從常態分佈。
c.均質性(Homoscedasticity) :給定Xi下,每個誤差項的變異數彼此都相等。
d.獨立性(Independence):誤差項應該為隨機的常態分佈,不同誤差彼此獨立無關聯。
e.無共線(Lack of multicollinearity):獨立變數間無高度相關性。
2) 誤差評估:
a.總變異(SST, Total sum of squares) =
殘差變異(SSE, Sum of squares due to error) + 迴歸變異(Sum of squares due to regression)
b. SSR / SST 越大,表示變異當中有越多的比例可以用迴歸模型解釋,表示模型適合度佳。
c. 殘差或稱均方誤差(MSE, Mean square error) = SSE / (n-2) ,用於量測誤差大小
d. 檢定統計量 F = SSR / MSE,當 F > F (0.95, 1 , n-2),則表示回歸模型顯著。
e. 個別參數可用 t檢定檢驗是否顯著。
f. 判斷係數 ( R^2, determinant of coefficient) = 1-(SSE/SST) , 可以用來判斷所建構模式的解釋能力。
g. 殘差圖(Residual diagram)是迴歸模式估計值對殘差的散佈圖,評估模型是否符合基本假設,如果符合基本假設,其散佈圖應該是不規律。
3) Multiple Linear Regression:
a.共線性(Multicollinearity):
獨立變數高度相關,雖然迴歸方程顯著,但獨立變數的迴歸係數估計偏差或不顯著,導致迴歸模型難以解釋。
b. 共線性的檢定可用變異數膨脹因子(VIF, Variance inflation factor ) = 1/(1-R^2)來衡量,一般若 VIF < 0.1 表示高度共線性。
c. 虛擬變數(Dummy variable:在迴歸分析(線性、羅吉斯…等)中,當自變項為類別變項時,研究者都要先進行虛擬編碼(Dummy code)的動作
d.自變項篩選方法:
#強迫進入法(All-possible):
不由系統篩選,所有自變項的,均須計算報告。通常作為初步分析使用。
#後退淘汰法(Backward elimination)
先將所有的自變項放入迴歸方程式中,然後根據淘汰標準一一將不符合標準的自變項加以淘汰
#前進選擇法(Forward Selection )
第一個進入迴歸方程式的自變項是與應變項有最大相關的自變項,第一個自變項進入模型之後,再以對判定係數值大小的影響,檢查第二個自變項該誰進入,依此類推,直到沒有其他的自變項符合選取的標準為止。
#雙向淘汰法(Bidirectional elimination)
#逐步迴歸法(Stepwise regression)
結合前進選擇法與反向淘汰法二種程序。首先採用順向選擇法,選進與應變項有最大相關的自變項,接下來以反向淘汰法檢查此自變項是否須加以排除。為了避免相同的自變項重複地被選進或排除,選進的標準(α值)必須小於淘汰的標準。




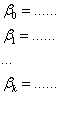








留言
張貼留言